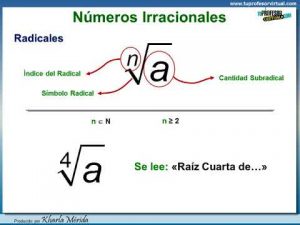
Llamamos números irracionales a los números que resulta imposible expresar a manera de números enteros. Estos van en completa discordancia con los números racionales, debido a la forma de su expresión.

Al momento de expresar los números irracionales a modo de decimal, estos números siguen siempre tras el punto decimal, evitando repetirse en cualquiera de los casos.

El descubrimiento de los números racionales

Hablar del descubrimiento de los números racionales implica situarse en los tiempo del griego Hipaso de Mataponto, a quien se le asocia con el descubrimiento de estos números durante el siglo V, A.C. Esto puede verificarse en un artículo publicado por la Universidad de Cambridge.

De acuerdo a la historia oficial, éste trabajaba en un problema matemático, cuando se topó con que a cierto rectángulo isósceles los dos lados de la base daban como resultado una unidad de longidud, con lo que obtuvo un número irracional, el cual es la hipotenusa √2.

De hecho, si se maneja el conocido teorema de pitágoras es posible comprobar esto de la siguiente forma: a^2 + b^2 = c^2.

La leyenda

Un detalle curioso con respecto a la leyenda de cómo se descubrieron los números irracionales es que se dice que Hipaso fue lanzado al mar. Esto se explica  causa de que pertenecía a los llamados «pitagóricos». En esta orden de carácter casi religioso se le atribuyen múltiples preceptos, entre los que se destaca el de «Todo son números«.

De acuerdo a esta creencia, el universo tal y como lo conocemos está compuesto por números enteros, algo que chocaba con el descubrimiento de los números irracionales. Los pitagóricos, perturbados por ello, habrían decidido castigar a Hipaso de dicha forma.